Trigonometry-Teaching Aid
Trigonometry Teaching Aid
Trigonometry is much easier to learn graphically. Each of the six trig functions is represented in the diagram of an arm sweeping around a circle shown in this flip book.

Imagine a 2-inch diameter circle. As an angle sweeps around the circle, all six trig functions can be seen increasing or decreasing.
 |
As the angle increases, the trig functions, change position (and therefore length) staying in relationship to the radius of one unit (1 inch, in this example) which corresponds to its numeral value listed for that trigonometric function. This animation is best be used as a teaching aid. Accuracy is limited to 1-2 places; however, excels at illustrating the way the values change as the angle changes. |
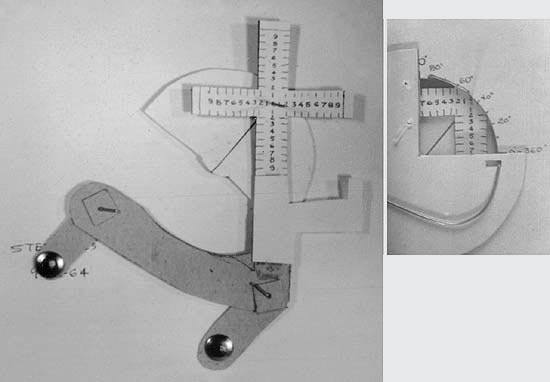
Early mockups from 1964:
Cardboard and thumbtack mockup.
For more information, please contact Steve Hines at:
USA
email: [email protected]
ph. 818-507-5812