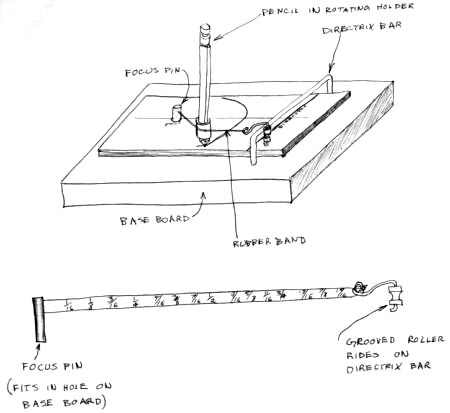
Conic-Section Teaching Device
Conic-Section Teaching Aid
This describes mathematical ratios in the family of conic curves (the parabola, ellipse, hyperbola, and circle), that result from slicing through a cone at different angles. The parabola results from slicing parallel to the axis. A hyperbola comes from slicing parallel to the side of the cone. The ellipse comes from cutting the cone obliquely. The circle is created by cutting the cone perpendicular to the cone’s axis.
 |
 |
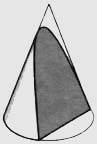
| Parabola | Ellipse |
 |
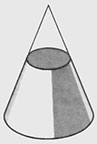 |
| Hyperbola | Circle |
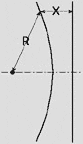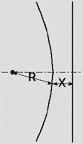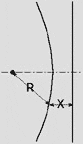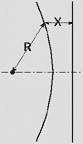
These conic sections are geometrically described as the locus of a point which maintains a certain ratio from a fixed point called the focus, and a straight line (the directrix). This ratio is different for each shape. The ratio for the parabola is fixed at 1:1.
The machine connected with these mathematical requirements allows the student to draw the ellipse, parabola, and the hyperbola using the proper ratio which is set on the machine by the student.
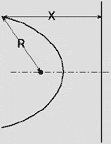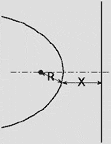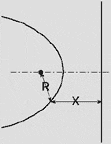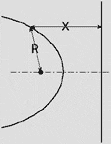
The parabola must have its point-to-the-focus distance equal to the point-to-the-directrix distance.
For the ellipse, the point-to-the-focus distance is less than the point-to-the-directrix distance.
In the hyperbola, the point-to-the-focus distance is greater than the point-to-the-directrix distance.
The circle is a special case. The circle drawn with this device will have a radius of zero.
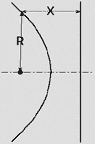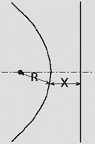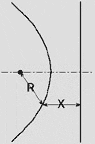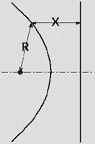 |
 |
 |
not aplicable |
|
Parabola R = X |
Ellipse R < X |
Hyperbola R > X |
Circle
|
The original sketches and models, made by Steve Hines in Sept. 1964.
To operate:
The pencil, in the rotating holder, is placed on the rubber band to the ratio desired within the range of the particular curve to be drawn and is swung around the focus, correcting the direction to prevent the pencil holder from rotating. If drawn carefully, the correct curve will be traced by the pencil on the pad of paper.
The stylus is held against the rubber band at a mark the represents the ratio of lengths on the rubber band to the focal point (FP) and to the directrix (PD). By maintaining the position on the rubber band while being stretched, the stylus draws the chosen conic section.