Mirror Stereo

Mirror-Stereo 3D

 

     This is a technique for taking stereoscopic 3-D pictures, using a simple mirror attachment, on any still film or digital camera.

 

    The Kodak Handle instant camera fitted with a Mirror-Stereo 3D adapter.  

---

 

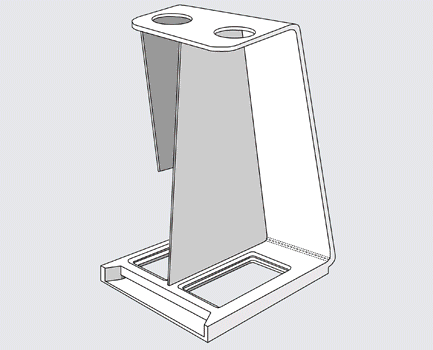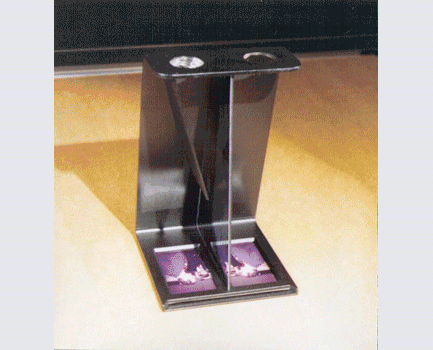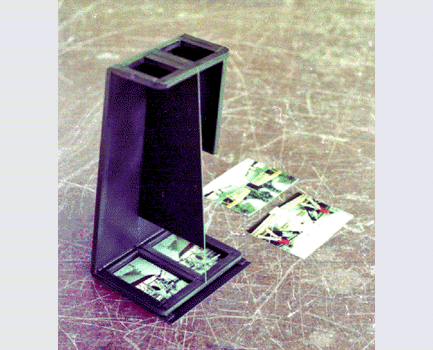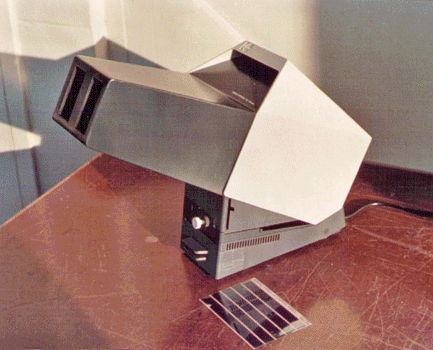
Mirror-Stereo 3D viewers:

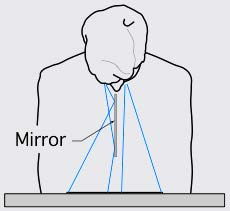
     The left eye sees the left image directly.  The right eye sees the reversed image reflected in the mirror.  The two images appear to be a single image, but with stereo depth.  This is where “two wrongs make a right” (seeing a mirror image of a mirror image).

---

 

---

 

Cameras adapted for Mirror-Stereo 3D:

 

     The Kodak Handle instant camera with a 3-D adapter.  Note the appearance of two lenses, one real, and one reflected in the mirror.  The stereo base is the distance between the real and reflected lenses.  

 

35mm SLR

      The threaded rod behind the mirror is turned to adjust the angle of the mirror, and therefore the convergence distance. This adjustment pulls or pushes the image in or out of the picture toward the viewer.

 

Kodak Pocket Instamatic 30 Camera

 

Bauer XL Super 8 movie camera

---

 

      This project is shown only to demonstrate past work by Steve Hines.